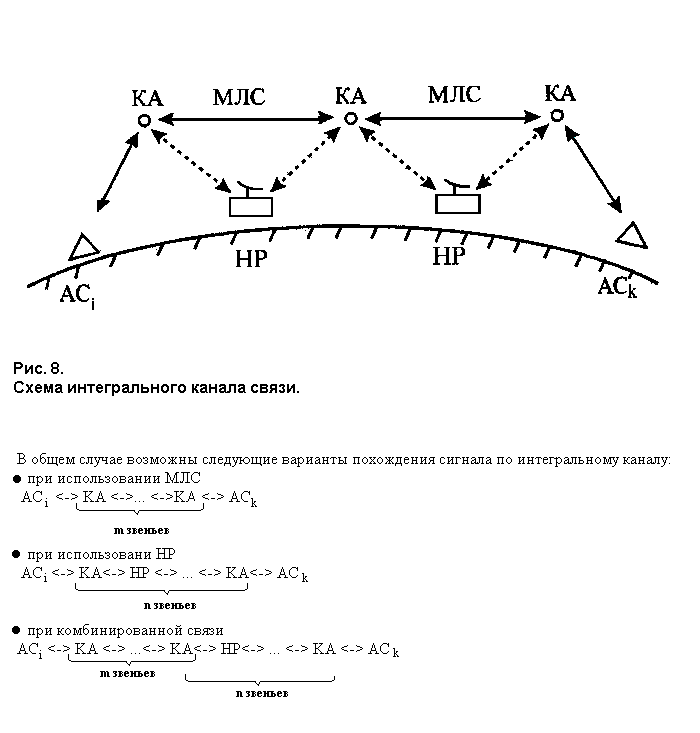
Необходимость расширения зоны обслуживания вплоть до глобальной и снижения энергетического потенциала в ССС заставляет рассматривать варианты их построения на базе группировок космических аппаратов (КА) на относительно низких, по сравнению с геостационарной, орбитах. В таких системах охват всей зоны обслуживания осуществляется совокупностью зон радиовидимости (ЗРВ) отдельных КА, входящих а группировку, вследствие чего возникает задача объединения их в единое целое, т.е. обеспечения связности системы, которая может достигаться или с помощью межепутниковых линий связи (МЛС) или наземных ретрансляторов (HP), или комбинацией этих двух способов. В любом варианте канал связи в многоспутниковой системе является интегральным.
На рис. 8 в качестве примера представлен интегральный канал связи от i-гo абонента k-му. абоненту с двумя звеньями ретрансляции, обеспечивающий связность либо с помощью МЛС (сплошные линии), либо с помощью HP (пунктирные линии).
Решение задачи обеспечения связности может иметь много вариантов, что приводит к необходимости ее оценки и выбору наиболее эффективного варианта.
Существуют различные определения связности и ее количественных оценок, но применительно к многоспутниковой системе эти определения требуют уточнения, поскольку в процессе движения КА по орбитам и вращения Земли взаимное положение элементов системы -(КА, HP, AC) постоянно изменяется во времени, а следовательно, изменяется во времени и структура системы.
Будем называть систему связной на некотором интервале времени, если в каждый его момент для любой пары объектов (абонентов системы), независимо от их положения в зоне обслуживания, существует возможность организации канала связи между ними с заданными параметрами.
Представим структуру системы в некоторый момент времени t виде графа G(Vs,Us), вершинами которого Vs являются элементы системы, а ветвями Us -связи между ними в момент времени t. Дополним этот граф еще двумя вершинами А и В, обозначающими некоторую пару объектов, и ветвями Ua и Ub, обозначающими их возможные связи в момент времени t с КА, в зонах которых они находятся.
Обозначим полученный граф как Gt(V, U), где V = (Vs, А, В); U = (Us, Ua, Ub). Каждой его вершине и ветви припишем веса W, отражающие изменение тех или иных параметров при прохождении сигнала через данный элемент. Такими параметрами могут быть: время задержки сигнала (в бортовых и наземных ретрансляторах, а также из-за распространения радиоволн), отношение сигнал/шум и др. Обобщающим параметром может служить число ретрансляций сигнала на пути от одного абонента к другому.
Длиной пути dk между двумя объектами системы по k-тому параметру назовем сумму весов W находящихся на данном пути вершин и ветвей. Условие связности двух объектов системы в неко торый момент времени t выполняется в том случае если в графе Gt (V, U) между его вершинами
А и В имеется хотя бы один путь длина которого dt (А, В) во каждому из К параметров, характеризующих качество канала, не превышает допустимого значения Dk :
Dk(A,B)
Действительно, если между двумя объектами существует более короткий, чем для другой пары, путь или имеется больше обходных (пусть и неполностью независимых) путей, тo связь между такими объектами будет более надежной, а оценка их связности выше.
Если бы система состояла из абсолютно надежных элементов и всегда находилась в полном составе, то наличие обходных путей между ее элементами или их отсутствие, как впрочем и их длина, если только она не больше допустимой, не имело бы значения.
Однако надежность всех элементов системы носит вероятностный характер, поэтому и уровень связности двух любых объектов на некотором интервале времени можно оценивать как вероятность существования на этом интервале хотя бы одного пути с допустимыми параметрами, а уровень связности системы - как среднее значение уровней связности всех возможных пар ее объектов.
При вычислении уровня связности двух объектов приходится находить пути, удовлетворяющие условию (*) в некоторые моменты времени t. Если качество канала оценивается совокупностью многих параметров, то задача становится весьма сложной. Однако в большинстве случаев достаточно ограничиться одним, наиболее критичным параметром, и тогда при проверке условия связности этих объектов достаточно найти кратчайший путь между ними и его длину по данному параметру. В дальнейшем рассматривается именно этот подход.
Методика определения уровня связности системы. Для этой цели воспользуемся методом статистических испытаний. Число испытаний выбирается исходя из требуемой точности получаемых результатов. Операции, выполняемые в каждом испытании осуществляются по следующему алгоритму:
После проведения выбранного числа испытаний по этому
алгоритму рассчитывается уровень связности системы как отношение числа испытаний, в которых выполняются условия связности, к их общему числу.
Рассмотрим подробнее некоторые позиции, данного алгоритма. Вопросы, связанные с генерированием случайных величин компьютерными методами, хорошо известны. Для этого необходимо лишь знать или задаться интегральными функциями распределения соответствующих величин.
Выбор пары обьектов можно осуществлять на основе различных моделей, учитывающих распределение объектов в зоне обслуживания, потоки информации между объектами, их взаимное расположение, время и т.д. Если точные данные ддя построения модели неизвестны, то целесообразно ориентироваться на наиболее простую модель, в которой плотность распределения объектов по зоне обслуживания принимается одинаковой, а вероятность связей между ними не зависит от их взаимного расположения и времени.
Структура линий МЛС обусловлена выполнением условий взаимной
радиовидимости между всеми КА и соответствием параметров линий МЛС наложенным на них ограничениям, связанных с возможностью и сложностью технической реализации антенных: систем ретрансляторов МЛС. Это в конечном счете приводит к ограничению допустимых значении изменений азимутального угла и угла места между взаимодействующими КА.
При нахождении связей между КА и наземными ретрансляторами для каждого из них выявляются все КА, в зонах которых в момент времени t находится данный HP, т.е. КА, расстояние от центров зон которых до соответствующего HP по поверхности Земли не превышает радиуса ЗРВ КА. Если таких КА всего два, то их выбор однозначен, если же больше двух, то выбираются два КА, соединение которых может с помощью HP наилучшим образом дополнить структуру МЛС.
Следует отметить, что эффективное использование HP (если только они не соединены между собой другими линиями связи, например, наземными) возможно лишь при условии их размещения в областях, где обеспечивается по крайней мере двукратное непрерывное покрытие земной поверхности зонами радиовидимости КА.
Процедура определения состояния системы в момент времени t зависит от модели описания поведения системы в процессе ее функционирования. Однако независимо от вида
модели и её характера (детерминированного или вероятностного) требуется знать сколько и какие именно элементы системы в данный момент времени находятся в работоспособном состоянии. Определение КА, в зонах которых располагаются выбранные объекты, т.е. абоненты системы, осуществляется так же, как и для HP.
Граф Gt(V,U) формируется на основании данных о наличии работоспособных элементов в системе, связях между ними и с объектами в момент времени t. Структуру графа удобно
представлять в виде матрицы связности, а информацию о весах его элементов - в виде матрицы весов.
Для нахождения кратчайшего пути между вершинами А и В целесообразно воспользоваться алгоритмом Дейкстры. Если длина найденного пути меньше допустимой, то условие связности в данном испытании выполняется. На основе полученных данных рассчитывается уровень связности системы, учитывающий состояние системы в процессе ее функционирования.
Порядок выбора орбитальной группировки и структуры системы. Облик системы, варианты организации ее связности, удовлетворяющие заданному уровню, обусловлены группировкой КА. Выбор орбитальной структуры - сложная задача и однозначного решения не имеет. Тем не менее можно предложить ряд рекомендаций.
Вначале необходимо отобрать орбитальные группировки, обеспечивающие однократный обзор зоны обслуживания при минимальном числе КА. При этом необходимо учитывать ряд факторов, которые влияют на ее параметры. Так, высота орбит КА зависит от предполагаемой энергетики радиолиний, имеющихся средств выведения КА на орбиту и др. Далее для каждой из набора выбранных группировок выясняется возможность обеспечения связности только за счет линий МЛС с учетом наложенных на них ограничений.
Приемлемой считается та группировка, которая обеспечивает в обслуживаемой зоне заданный уровень связности. Если же ни одна из группировок КА не дает желаемого результата при использовании МЛС, то в состав системы связи, следует ввести наземные ретрансляторы. Число НР и схема их расположения должны определяться отдельно в каждбм конкретном случае.
После введения HP вновь рассчитывается уровень связности систем с комбинированным использованием МЛС и HP при различных вариантах размещения HP. Если и в этом случае ни для| одной группировки не достигается заданный уровень связности, то в таком же порядке необходимо исследовать другой набор группировок, уже с большим числом КА.
В качестве примера рассмотрим выбор группировки КА для системы связи, предназначенной для обслуживания широтного пояса 35...70° с.ш. и обеспечивающей уровень связности, равный единице при числе ретрансляций не более четырех. При этом будем считать, что объекты системы располагаются зоне обслуживания с одинаковой плотностью, а распределение потоков информации между ними не зависит от их взаимного расположения и времени. На линии МЛС введем ограничение -
отклонение азимутального угла антенны не должно превышать 50°.
Выберем высоту орбиты КА 1640 км и наклонение 63°. Анализ связности системы проведем на интервале времени, равном одним суткам, и в предположении, что система в этот период находится в полном составе.
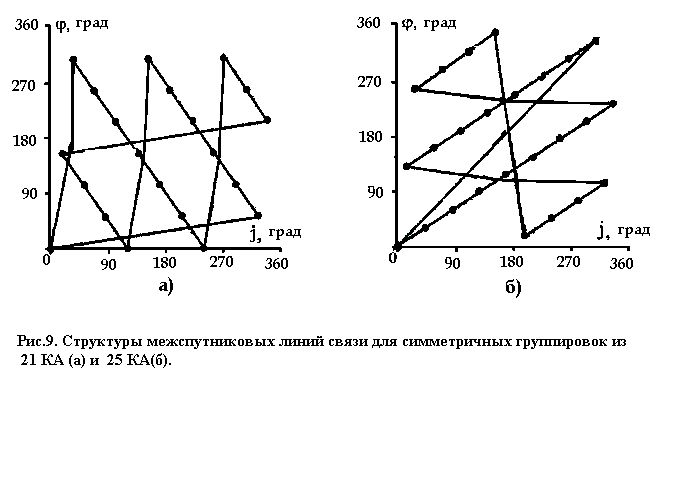
Для простоты анализа рассмотрим всего две группировки, обеспечивающие непрерывный обзор зоны обслуживания. Первая состоит из 21 КА с одним КА на каждой орбите, с долготами восходящих узлов jn=360*2*(n-1)/21 и начальными аргументами широты jn = -360*3*(n-1)/21, где n-номер КА. Вторая группировка состоит из 25 КА с одним КА на каждой орбите и параметрами jn= 360*3 (n-1)/25 и (j = -З60*2*(n-1)/25). Применим предложенную выше методику, используя вначале только линии МЛС.
На рис9. представлены группировки КА и структуры МЛС для первой (а) и второй (б) систем связи, где по оси абсцисс отложены долготы восходящих узлов j, а по оси ординат - начальные аргументы широты j. Заданным требованиям здесь удовлетворяют только МЛС, объединяющие все КА в одну "цепочку".
На рис. 10. показаны зависимости уровня связности от допустимого числа
ретрансляций в системе D при использовании только линий МЛС. При четырёх ретрансляциях ни одна из систем не обеспечивает заданного уровня связности, равного единице, хотя вторая система (б) близка к этому значению: Для уменьшения, числа ретрансляций введем в систему свзи HP (в состав первой системы - шесть ретрансляторов, второй - четыре, равномерно распределенные по долготам на 55° с.ш.).
На рис. 11. показаны зависимости уровня связности систем скомбинированным споcобом использования линий МЛС и HP от допустимого числа ретрансляций. Из анализа этих зависимостей видно, что в первой системе уровень связности 1,0 достигается при девяти ретрансляциях, а во второй (б) - при трех.
Предложенный в работе показатель уровня связности для систем спутниковой связи, использующих группировки космических аппаратов иа круговых орбитах, позволяет we только сравнивать между собой различные системы такого вида, ноиосуществлять выбор группировок КА, обеспечивающих наивыгоднейшие условия для связности при проектировании системы с заданными параметрами.
предыдущая страница |
начало |
следующая страница |
глоссарий
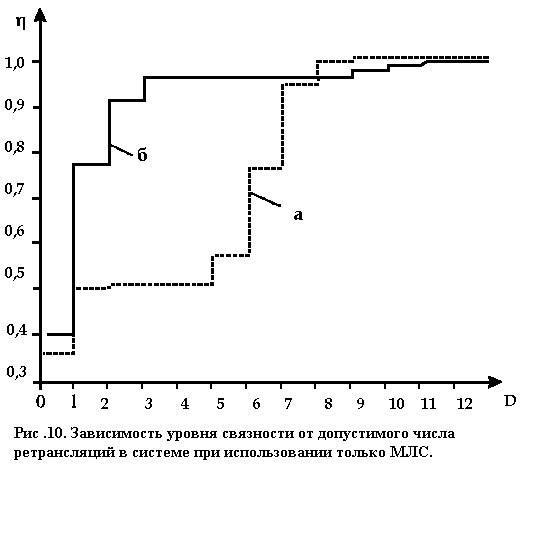
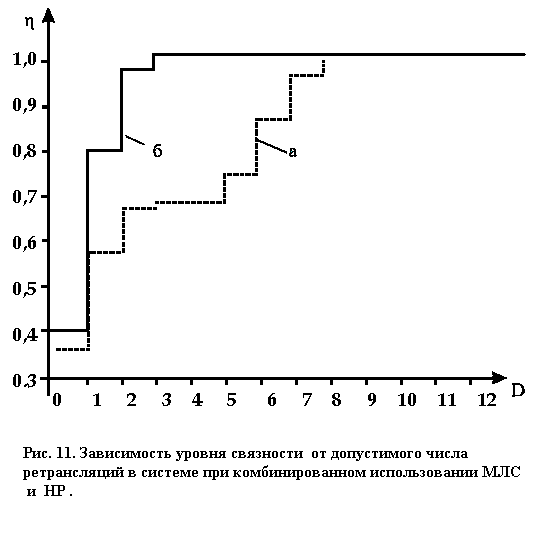Таким образом, первая система, хотя и имеет выигрыш перед второй по числу КА в группировке, не обеспечивает необходимого уровня связности при заданном числе ретрансляций (не более 4) ни при использовании только линий МЛС, ни при введении дополнительно наземных ретрансляторов. Вторая же система при комбинированном использовании линий МЛС и HP удовлетворяет этим требованиям уже при числе ретрансляций, равном 3.