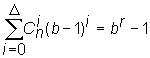 , где
D
- максимальная кратность исправляемых ошибок; b - основание кода; r - число проверочных
символов.
, где
D
- максимальная кратность исправляемых ошибок; b - основание кода; r - число проверочных
символов.Преобразование дискретного сообщения в сигнал обычно осуществляется в виде двух операций - кодирования и модуляции. Кодирование представляет собой преобразование сообщения в последовательность кодовых символов.
Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Их совокупность называется алфавитом источника сообщения. Так как число элементов в алфавите конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел.
Так, для передачи букв русского алфавита (их 32) необходимо передать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача одной из десяти цифр от 0 до 9 для каждого десятичного разряда. То есть для передачи букв русского алфавита нужно иметь техническую возможность передачи и приема десяти различных сигналов, соответствующих различным цифрам.
На практике при кодировании дискретных сообщений широко применяется двоичная система счисления.
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, обозначающих дискретные сообщения, образует код.
Правило кодирования может быть выражено кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации. Множество возможных кодовых символов называется кодовым алфавитом, а их количество m - основанием кода.
В общем случае при основании кода m правила кодирования N элементов сообщения сводятся к правилам записи N различных чисел в m-ичной системе счисления. Число разрядов n, образующих кодовую комбинацию, называется значностью кода, или длиной кодовой комбинации. В зависимости от системы счисления, используемой при кодировании, различают двоичные и m-ичные (недвоичные) коды.
Коды, у которых все комбинации имеют одинаковую длину, называют равномерными. Для равномерного кода число возможных комбинаций равно mn. Примером такого кода является пятизначный код Бодо, содержащий пять двоичных элементов (m=2, n=5). Число возможных кодовых комбинаций равно 25=32, что достаточно для кодирования всех букв алфавита. Применение равномерных кодов не требует передачи разделительных символов между кодовыми комбинациями.
Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов, но и их количеством. Это приводит к тому, что различные комбинации имеют различную длительность. Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются только в двух сочетаниях - как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам - тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями.
По помехоустойчивости коды делят на простые (примитивные) и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются простыми, или кодами без избыточности. В простых равномерных кодах превращение одного символа комбинации в другой, например 1 в 0 или 0 в 1, приводит к появлению новой комбинации, т. е. к ошибке.
Корректирующие коды строятся так, что для передачи сообщения используются не все кодовые комбинации mn, а лишь некоторая часть их (так называемые разрешенные кодовые комбинации). Тем самым создается возможность обнаружения и исправления ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются введением в кодовые комбинации дополнительных (избыточных) символов.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называют соответственно кодером и декодером. Как правило, кодер и декодер выполняются физически в одном устройстве, называемым кодеком.
Рассмотрим основные принципы построения корректирующих кодов или помехоустойчивого кодирования.
Напомним, что расстоянием Хэмминга между двумя кодовыми n-последовательностями, biи bj, которое будем далее обозначать d(i; j), является число разрядов, в которых символы этих последовательностей не совпадают.
Говорят, что в канале произошла ошибка кратности q, если в кодовой комбинации q символов приняты ошибочно. Легко видеть, что кратность ошибки есть не что иное, как расстояние Хэмминга между переданной и принятой кодовыми комбинациями, или, иначе, вес вектора ошибки.
Рассматривая все разрешенные кодовые комбинации и определяя кодовые расстояния между каждой парой, можно найти наименьшее из них d = min d(i; j), где минимум берется по всем парам разрешенных комбинаций. Это минимальное кодовое расстояние является важным параметром кода. Очевидно, что для простого кода d=1.
Обнаруживающая способность кода характеризуется следующей теоремой. Если код имеет d>1 и используется декодирование по методу обнаружения ошибок, то все ошибки кратностью q<d обнаруживаются. Что же касается ошибок кратностью q³ d, то одни из них обнаруживаются, а другие нет.
Исправляющая способность кода при этом правиле декодирования определяется следующей теоремой. Если код имеет d>2 и используется декодирование с исправлением ошибок по наименьшему расстоянию, то все ошибки кратностью q<d/2 исправляются. Что же касается ошибок большей кратности, то одни из них исправляются, а другие нет.
Задача кодирования состоит в выборе кода, обладающего максимально достижимым d. Впрочем, такая формулировка задачи неполна. Увеличивая длину кода n и сохраняя число кодовых комбинаций М, можно получить сколь угодно большое значение d. Но такое "решение" задачи не представляет интереса, так как с увеличением n уменьшается возможная скорость передачи информации от источника.
Если длина кода n задана, то можно получить любое значение d, не превышающее n, уменьшая число комбинаций М. Поэтому задачу поиска наилучшего кода (в смысле максимального d) следует формулировать так: при заданных M и n найти код длины n, содержащий М комбинаций и имеющий наибольшее возможное d. В общем виде эта задача в теории кодирования не решена, хотя для многих значений n и М ее решения получены.
На первый взгляд помехоустойчивое кодирование реализуется весьма просто. В память кодирующего устройства (кодера) записываются разрешенные кодовые комбинации выбранного кода и правило, по которому с каждым из М сообщений источника сопоставляется одна из таких комбинаций. Данное правило известно и декодеру.
Получив от источника определенное сообщение, кодер отыскивает соответствующую ему комбинацию и посылает ее в канал. В свою очередь, декодер, приняв комбинацию, искаженную помехами, сравнивает ее со всеми М комбинациями списка и отыскивает ту из них, которая ближе остальных к принятой.
Однако даже при умеренных значениях n такой способ весьма сложный. Покажем это на примере. Пусть выбрана длина кодовой комбинации n=100, а скорость кода примем равной 0.5 (число информационных и проверочных символов равно). Тогда число разрешенных комбинаций кода будет 250»1015. Соответственно размер таблицы будет 100´ 1015=1017 бит » 1016 байт = 10000 Тбайт.
Таким образом, применение достаточно эффективных (а значит, и достаточно длинных) кодов при табличном методе кодирования и декодирования технически невозможно.
Поэтому основное направление теории помехоустойчивого кодирования заключается в поисках таких классов кодов, для которых кодирование и декодирование осуществляются не перебором таблицы, а с помощью некоторых регулярных правил, определенных алгебраической структурой кодовых комбинаций.
Одним из таких классов являются линейные блоковые коды. Линейными называются такие двоичные коды, в которых множество всех разрешенных блоков является линейным пространством относительно операции поразрядного сложения по модулю 2.
Если записать k линейно-независимых блоков в виде k строк, то получится матрица размером n´ k, которую называют порождающей или производящей матрицей кода G.
Множество линейных комбинаций образует линейное пространство, содержащее 2k блоков, т.е. линейный код, содержащий 2k блоков длиной n, обозначают (n, k). При заданных n и k существует много различных (n, k)-кодов с различными кодовыми расстояниями d, определяемых различными порождающими матрицами. Все они имеют избыточность e k=1-k/n или относительную скорость Rk=k/n.
Чаще всего применяют систематические линейные коды, которые строят следующим образом. Сначала строится простой код длиной k, т.е. множество всех k-последовательностей двоичных символов, называемых информационными. Затем к каждой из этих последовательностей приписывается r = n - k проверочных символов, которые получаются в результате некоторых линейных операций над информационными символами.
Простейший систематический код (n,n-1) строится добавлением к комбинации из n-1 информационных символов одного проверочного, равного сумме всех информационных символов по модулю 2. Такой код (n,n-1) имеет d=2 и позволяет обнаружить одиночные ошибки и называется кодом с одной проверкой на четность.
Преимуществом линейных, в частности систематических, кодов является то, что в кодере и декодере не нужно хранить большие таблицы всех кодовых комбинаций, а при декодировании не нужно производить большое количество сравнений.
Однако, для получения высокой верности связи следует применять коды достаточно большой длины. Применение систематического кода в общем случае, хотя и позволяет упростить декодирование по сравнению с табличным способом, все же при значениях n порядка нескольких десятков не решает задачу практической реализации.
Совершенными (плотно упакованными) называют коды, в которых выполняются
соотношения 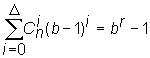 , где
D
- максимальная кратность исправляемых ошибок; b - основание кода; r - число проверочных
символов.
, где
D
- максимальная кратность исправляемых ошибок; b - основание кода; r - число проверочных
символов.
Они отличаются тем, что позволяют исправлять все ошибки кратностью D или меньше и ни одной ошибки кратности больше D.
Число известных совершенных кодов ограничено кодами Хэмминга значности
![]() и бинарным циклическим кодом Голея.
и бинарным циклическим кодом Голея.
Квазисовершенными принято называть коды, исправляющие все ошибки
кратности D
и ![]() ошибок
кратности D
+1 при условии, что
ошибок
кратности D
+1 при условии, что 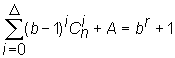 .
.
Класс квазисовершенных кодов значительно шире, чем класс плотно упакованных кодов.
Совершенные и квазисовершенные коды обеспечивают максимум вероятности правильного приема комбинации при равновероятных ошибках в канале связи.
Был предложен ряд кодов и способов декодирования, при которых сложность декодера растет не экспоненциально, а лишь как некоторая степень n. В классе линейных систематических двоичных кодов это - циклические коды. Циклические коды просты в реализации и при невысокой избыточности обладают хорошими свойствами обнаружения ошибок. Циклические коды получили очень широкое распространение как в технике связи, так и в компьютерных средствах хранения информации. В зарубежных источниках циклические коды обычно называют избыточной циклической проверкой (CRC, Cyclic Redundancy Check).
Рассмотрим данный класс кодов подробнее. Название циклических кодов связано с тем, что каждая кодовая комбинация, получаемая путем циклической перестановки символов, также принадлежит коду. Так, например, циклические перестановки комбинации 1000101 будут также кодовыми комбинациями 0001011, 0010110, 0101100 и т.д.
Представление кодовых комбинаций в виде многочленов F(x) позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2. Деление осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложения по модулю 2. Циклическая перестановка кодовой комбинации эквивалентна умножению полинома F(x) на x с заменой на единицу переменной со степенью, превышающую степень полинома.
Любой полином G(x) степени r<n, который делит без остатка двучлен xn - 1, может быть порождающим полиномом циклического (n,k)-кода, где k = n - r. В этот код входят те полиномы, которые без остатка делятся на G(x).
Особую роль в теории циклических кодов играют неприводимые многочлены G(x), т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней.
Идея построения циклического кода (n,k) сводится к тому, что полином Q(x), представляющий информационную часть кодовой комбинации, нужно преобразовать в полином F(x) степени не более n -1, который без остатка делится на порождающий полином G(x) (неприводимый многочлен) степени r = n - k. Рассмотрим последовательность операций построения циклического кода.
Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x).
Умножаем Q(x) на одночлен xrи получаем Q(x)xr.
Делим полином Q(x)xr на порождающий полином G(x) степени r, при этом получаем частное от деления C(x) такой же степени, что и Q(x).
![]() где R(x) - остаток от
деления Q(x)xr на G(x).
где R(x) - остаток от
деления Q(x)xr на G(x).
Умножив обе части на G(x), получим ![]() .
.
Полином F(x) делится без остатка на G(x), т.е. представляет собой разрешенную комбинацию циклического (n,k)-кода.
Таким образом, разрешенную кодовую комбинацию циклического кода можно получить двумя способами: умножением кодовой комбинации простого кода C(x) на полином G(x) или умножением кодовой комбинации Q(x) простого кода на одночлен xr и добавлением к этому произведению остатка R(x).
В первом случае информационные и проверочные разряды не отделены друг от друга (код получается неразделимым). Во втором случае получается разделимый код. Этот код достаточно широко используется на практике, поскольку процесс декодирования и обнаружения ошибок при использовании разделимого кода выполняется проще.
Рассмотрим пример разделяемого циклического кода (9,5) с порождающим полиномом
![]()
![]() . В качестве информационной части кодовой комбинации возьмем полином
. В качестве информационной части кодовой комбинации возьмем полином
![]() .
.
Умножение Q(x) на xr эквивалентно повышению степени многочлена на r.
Q(x) = ![]() ®
10111.
®
10111.
Q(x)xr = ![]() ®
101110000
®
101110000
Формирование проверочной группы осуществляется в процессе деления Q(x)xr на G(x).
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | ||||
| 0 | 1 | 0 | 0 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 0 | 0 | 1 | 1 | |||||||||
| 0 | 0 | 1 | 1 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 0 | 1 | 1 | 0 | 0 | |||||||||
| 0 | 0 | 0 | 0 | 0 | |||||||||
| 1 | 1 | 0 | 0 |
В результате деления получаем частное от деления
C(x) = x4+x2 ®
10100 и остаток от деления R(x) = x3+x2
®
1100. Для получения разрешенной кодовой комбинации остаток (проверочная группа) помещается на
место "пустых" разрядов Q(x)xr, т.е.
F(x)= ![]() ®
101111100. Данная комбинация отправляется в канал связи.
Аналогичные операции выполняются для других информационных комбинаций.
®
101111100. Данная комбинация отправляется в канал связи.
Аналогичные операции выполняются для других информационных комбинаций.
Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок.
При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.
Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью и будут рассмотрены ниже в подразделе 6.1.2.8.
Наряду с циклическими кодами на практике используются другие типы кодов, обладающие различными свойствами. Подробное рассмотрение классов кодов выходит за рамки настоящего курса, поэтому приведем только их краткую характеристику.
Среди циклических кодов особое значение имеет класс кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза - Чоудхури - Хоквингема (обозначаемые сокращением БЧХ) отличаются сравнительно просто реализуемой процедурой декодирования.
Относительно простой является процедура мажоритарного декодирования, применимая для некоторого класса двоичных линейных, в том числе циклических кодов. Основана она на том, что в этих кодах каждый информационный символ можно несколькими способами выразить через другие символы кодовой комбинации.
Мощные коды (т.е. коды с длинными блоками и большим кодовым расстоянием d) при сравнительно простой процедуре декодирования можно строить, объединяя несколько коротких кодов. Так строится, например, итеративный код из двух линейных систематических кодов (n1,k1) и (n2,k2). Минимальное кодовое расстояние для двумерного итеративного кода d=d1d2, где d1 и d2 - соответственно минимальные кодовые расстояния для кодов 1-й и 2-й ступеней.
На итеративный код похож каскадный код, но между ними имеется существенное различие. Первая ступень кодирования в каскадном коде является линейным систематическим двоичным кодом (внутренний код), каждая комбинация которого рассматривается как один символ недвоичного кода второй ступени (внешнего). При приеме сначала декодируются (с обнаружением или исправлением ошибок) все строки (блоки) внутреннего кода, а затем декодируется блок внешнего m-ичного кода, причем исправляются ошибки и стирания, оставшиеся после декодирования внутреннего кода. В качестве внешнего кода используют обычно m-ичный код Рида-Соломона, который является подклассом кодов БЧХ и обеспечивает наибольшее возможное d при заданных n2 и k2, если n2<m. Каскадные коды во многих случаях наиболее перспективны среди известных блочных помехоустойчивых кодов.
Для каналов с группированием ошибок часто применяют метод перемежения символов, или декорреляции ошибок. Он заключается в том, что символы, входящие в одну кодовую комбинацию, передаются не непосредственно друг за другом, а перемежаются символами других кодовых комбинаций.
Если интервал между символами, входящими в одну комбинацию, сделать больше максимально возможной длины группы ошибок, то в пределах комбинации группирования ошибок не будет. Группа ошибок распределится в виде одиночных ошибок на группу комбинаций. Одиночные ошибки будут легко обнаружены (исправлены) декодером.
Нередко встречаются случаи, когда информация может передаваться не только от одного абонента к другому, но и в обратном направлении. В таких условиях появляется возможность использовать обратный поток информации для существенного повышения верности сообщений, переданных в прямом направлении. При этом не исключено, что по обоим каналам (прямому и обратному) в основном непосредственно передаются сообщения в двух направлениях ("дуплексная связь") и только часть пропускной способности каждого из каналов используют для передачи дополнительных данных, предназначенных для повышения верности.
Возможны различные способы использования системы с обратной связью в дискретном канале. Обычно их подразделяют на два типа: системы с информационной обратной связью и системы с управляющей обратной связью.
Системами с информационной обратной связью (ИОС) называются такие, в которых с приемного устройства на передающее поступает информация о том, в каком виде принято сообщение. На основании этой информации передающее устройство может вносить те или иные изменения в процесс передачи сообщения:
В системах с управляющей обратной связью (УОС) приемное устройство на основании анализа принятого сигнала само принимает решение о необходимости повторения, изменения способа передачи, временного перерыва связи и передает об этом указание передающему устройству. Возможны и смешанные методы использования обратной связи, когда в некоторых случаях решение принимается на приемном устройстве, а в других случаях на передающем устройстве на основании полученной по обратному каналу информации.
Наиболее распространены системы с УОС при использовании одновременно с обнаружением ошибок. Такие системы часто называют системами с переспросом, или с автоматическим запросом ошибок (ARQ, Automatic Repeat reQuest).
Реклама:
Amf доставка цветов в омск www.florida55.ru.